Čo je doba trvania Macaulay?
Macaulay Duration je doba, ktorú investor potrebuje na to, aby získal späť svoje investované peniaze do dlhopisu prostredníctvom kupónov a splácania istiny. Táto doba predstavuje vážený priemer obdobia, počas ktorého by mal investor zostať investovaný do cenného papiera, aby sa súčasná hodnota peňažných tokov z investície zhodovala so sumou zaplatenou za dlhopis.
Macaulayova doba trvania je veľmi dôležitý faktor, ktorý je potrebné zohľadniť pred kúpou dlhového nástroja. Môže to výrazne pomôcť investorom pri výbere z rôznych súborov dostupných cenných papierov s pevným výnosom na trhu. Ako všetci vieme, ceny dlhopisov nepriamo súvisia s úrokovými sadzbami. Investori majú dobrý prehľad o tom, aký dlhopis kúpiť, dlhodobejší alebo kratší, ak poznajú duráciu, ktorú ponúkajú rôzne kupónové dlhopisy spolu s projektovanou štruktúrou úrokových sadzieb.
Macaulayova doba trvania
Môže sa vypočítať pomocou nasledujúceho vzorca,
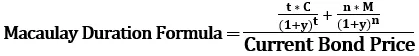

Kde,
- t = časové obdobie
- C = platba kupónom
- y = výnos
- n = počet období
- M = zrelosť
- Aktuálna cena dlhopisu = súčasná hodnota peňažných tokov
Výpočet trvania Macaulaya s príkladom
Pozrime sa na príklad trvania Macaulaya, aby sme tomu lepšie porozumeli.
Za dlhopis v hodnote 1 000 dolárov sa platí 8% kupónová sadzba a splatnosť je štyri roky. Sadzba kupónu je 8% pa Pri polročnej platbe. Môžeme očakávať, že nastanú nasledujúce peňažné toky.
- 6 mesiacov: 40 dolárov
- 1 rok: 40 dolárov
- 1,5 roka: 40 dolárov
- 2 roky: 40 dolárov
- roky: 40 dolárov
- 3 roky: 40 dolárov
- 3,5 roka: 40 dolárov
- 4 roky: 1 040 dolárov
Vypočítajte dobu trvania Macaulay
Riešenie:
S vyššie uvedenými informáciami môžeme vypočítať faktor zľavy. Na odvodenie diskontného faktora môžeme použiť nasledujúci polročný úrokový vzorec. 1 / (1 + r) n, kde r je kupónová sadzba an je počet zložených období.
Faktor zľavy
Výpočet diskontných faktorov na 6 mesiacov bude -

Faktory zľavy na 6 mesiacov = 1 / (1 + 8% / 2)
Faktory zľavy = 0,9615
Podobne môžeme urobiť výpočet diskontného faktora pre roky 1 až 4.

Súčasná hodnota peňažných tokov
Súčasná hodnota hotovostného toku po dobu 6 mesiacov bude -

Teraz, aby sme získali súčasnú hodnotu peňažných tokov, musíme vynásobiť peňažné toky za každé obdobie ich príslušným diskontným faktorom.
Aktuálna hodnota peňažného toku za 6 mesiacov: 1 x 40 $ x 0,9615
Súčasná hodnota hotovostného toku = 38,46 USD
Podobne môžeme urobiť výpočet súčasnej hodnoty peňažných tokov za 1. až 4. rok.

Macaulay Trvanie
Výpočet trvania Macaulaya bude -

- Aktuálna cena dlhopisu = PV všetkých peňažných tokov 6 079,34
- Trvanie Macaulaya = 6 079,34 USD / 1 000 USD = 6,07934
Podrobný výpočet trvania Macaulaya môžete nájsť v danej šablóne programu Excel vyššie.
Prednosti použitia doby trvania
Dĺžka trvania hrá dôležitú úlohu pri pomoci investorom pochopiť rizikový faktor dostupnej bezpečnosti s pevným výnosom. Rovnako ako sa meria riziko v akciách odchýlkou od priemeru alebo jednoducho odvodením beta zabezpečenia, riziko v nástrojoch s pevným výnosom sa striktne odhaduje podľa Macaulayovej doby trvania nástroja.
Pochopenie a porovnanie Macaulaya Trvanie nástrojov môže trvať dlhú cestu pri výbere vhodného riešenia pre vaše portfólio s pevným príjmom.
Prekážky používania trvania
Duration je dobrá aproximácia cenových zmien dlhopisu bez opcie, ale je dobrá iba pre malé zmeny úrokových sadzieb. S pribúdajúcimi zmenami sadzieb sa stáva zakrivenie vzťahu ceny a výnosu dlhopisu dôležitejšie. Inými slovami, lineárny odhad cenových zmien, napríklad trvanie, bude obsahovať chyby.
V skutočnosti vzťah medzi cenou dlhopisu a výnosom nie je lineárny, ale konvexný. Táto konvexnosť ukazuje, že rozdiel medzi skutočnými a odhadovanými cenami sa zväčšuje s rastúcimi výnosmi. To znamená, že rozšírenie chyby v odhadovanej cene je spôsobené zakrivením skutočnej cenovej cesty. Toto sa nazýva stupeň konvexnosti.
Spodná čiara
Znalosti o trvaní Macaulaya sú prvoradé pri zisťovaní budúcich výnosov z nástrojov s pevným príjmom. Preto je veľmi vhodné, aby investori, najmä investori s averziou k riziku, vyhodnotili a porovnali trvanie ponúkané rôznymi dlhopismi, aby dosiahli minimálnu kombináciu odchýlok a dosiahli maximálny výnos s čo najmenším rizikom. Pred rozhodnutím o kúpe by ste mali zvážiť aj faktor úrokovej sadzby.








