Čo je korelačný koeficient?
Korelačný koeficient sa používa na určenie toho, aký silný je vzťah medzi dvoma premennými a jeho hodnoty sa môžu pohybovať od -1,0 do 1,0, kde -1,0 predstavuje negatívnu koreláciu a +1,0 predstavuje pozitívny vzťah. Zvažuje relatívne pohyby v premenných a potom definuje, či medzi nimi existuje nejaký vzťah.
Vzorec korelačného koeficientu
r = n (∑xy) - ∑x ∑y / √ (n * ( 2x 2 - (∑x) 2 )) * (n * (2y 2 - (∑y) 2 ))
Kde
- r = korelačný koeficient
- n = počet pozorovaní
- x = 1. premenná v kontexte
- y = 2. premenná
Vysvetlenie
Ak existuje nejaká korelácia alebo povedzme vzťah medzi dvoma premennými, potom to znamená, že ak sa jedna z premenných mení v hodnote, potom aj druhá premenná bude mať tendenciu meniť sa v hodnote, povedzme v konkrétnej, ktorá môže byť buď v rovnakej alebo v opačným smerom. Čitateľská časť rovnice vedie test a relatívnu silu premenných, ktoré sa pohybujú spoločne, a menovateľská časť rovnice upravuje mierku čitateľa vynásobením rozdielov premenných od štvorcových premenných.
Príklady
Príklad č
Zvážte nasledujúce dve premenné, xay, od ktorých sa vyžaduje, aby ste vypočítali korelačný koeficient.
Ďalej sú uvedené údaje pre výpočet.

Riešenie:
Pomocou vyššie uvedenej rovnice môžeme vypočítať nasledujúce

Všetky hodnoty v tabuľke vyššie máme n = 4.
Zadajme teraz hodnoty pre výpočet korelačného koeficientu.

Preto je výpočet nasledovný,

r = (4 * 25 032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30 058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Koeficient bude -

Koeficient = 0,99932640
Príklad č
Krajina X je krajina s rastúcou ekonomikou a chce vykonať nezávislú analýzu rozhodnutí svojich centrálnych bánk týkajúcich sa zmien úrokových sadzieb, či už tieto zmeny ovplyvnili infláciu a či ich centrálna banka dokáže kontrolovať.
Ďalej uvádzame zhrnutie úrokovej sadzby a miery inflácie, ktoré v krajine priemerne za tieto roky prevládali.
Ďalej sú uvedené údaje pre výpočet.

Prezident krajiny vás požiadal, aby ste vykonali analýzu a predstavili ju na nasledujúcom stretnutí. Použite koreláciu a určite, či centrálna banka splnila svoj cieľ alebo nie.
Riešenie:
Pomocou vyššie diskutovaného vzorca môžeme vypočítať korelačný koeficient. Zaobchádzanie s úrokovou mierou ako s jednou premennou, napríklad x, a s mierou inflácie ako s ďalšou premennou, ako s y.

Všetky hodnoty v tabuľke vyššie máme n = 6.
Zadajme teraz hodnoty pre výpočet korelačného koeficientu.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Korelácia bude -

Korelácia = -0,92
Analýza: Ukazuje sa, že korelácia medzi úrokovou mierou a mierou inflácie je negatívna, čo sa javí ako správny vzťah. So zvyšovaním úrokovej sadzby klesá inflácia, čo znamená, že majú tendenciu sa pohybovať opačným smerom a z uvedeného výsledku vyplýva, že centrálna banka bola úspešná pri realizácii rozhodnutia týkajúceho sa úrokovej politiky.
Príklad č
Laboratórium ABC vedie výskum výšky a veku a chcelo by sa zistiť, či medzi nimi existuje nejaký vzťah. Zhromaždili vzorku 1000 ľudí pre každú z kategórií a prišli s priemernou výškou v tejto skupine.
Ďalej sú uvedené údaje pre výpočet korelačného koeficientu.

Je od vás požadované, aby ste vypočítali korelačný koeficient a dospeli k záveru, že ak nejaký vzťah existuje.
Riešenie:
Zaobchádzanie s vekom ako s jednou premennou, povedzme x, a zaobchádzanie s výškou (v cms) ako s ďalšou premennou ako y.

Všetky hodnoty v tabuľke vyššie máme n = 6.
Zadajme teraz hodnoty pre výpočet korelačného koeficientu.

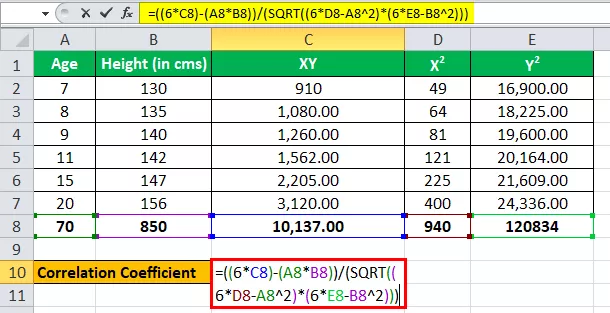
r = (6 * 10 137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1 20 834) - (850) 2 )
r = 1 322,00 / 1 361,23
Korelácia bude -

Korelácia = 0,971177099
Relevantnosť a použitie
Používa sa v štatistike hlavne na analýzu sily vzťahu medzi premennými, ktoré sa zvažujú, a ďalej tiež meria, či existuje lineárny vzťah medzi danými súbormi údajov a tým, ako dobre by mohli súvisieť. Jedným z bežných opatrení, ktoré sa používajú v korelácii, je Pearsonov korelačný koeficient.
Ak sa premenná zmení v hodnote a spolu s touto ďalšou premennou sa zmení v hodnote, potom je pochopenie tohto vzťahu kritické, pretože na predpovedanie zmeny hodnoty druhej premennej je možné použiť hodnotu prvej premennej. Korelácia má v dnešnej modernej dobe mnoho rôznych využití, napríklad vo finančnom priemysle, vo vedeckom výskume a kde nie. Je však dôležité vedieť, že korelácia má tri hlavné typy vzťahov. Prvým z nich je pozitívny vzťah, v ktorom sa uvádza, že ak dôjde k zmene hodnoty premennej, dôjde k zmene súvisiacej premennej rovnakým smerom. Podobne, ak existuje negatívny vzťah, potom sa príbuzná premenná bude správať opačným smerom. Ak tiež neexistuje korelácia, potom r bude znamenať nulovú hodnotu.Na lepšom pochopení tohto konceptu sa pozrite na obrázkoch nižšie.









