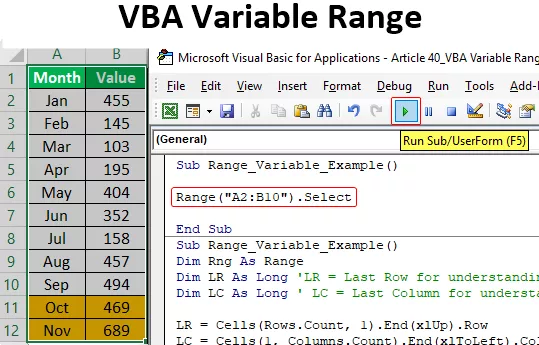
Vzorec na výpočet exponenciálneho rastu
Konečná hodnota = Počiatočná hodnota * (1 + Ročná miera rastu / Počet zložení ) Počet rokov * Počet zloženiaExponenciálny rast označuje nárast v dôsledku zloženia údajov v čase, a preto sleduje krivku, ktorá predstavuje exponenciálnu funkciu.

V prípade kontinuálneho zloženia sa však na výpočet konečnej hodnoty použije rovnica vynásobením počiatočnej hodnoty a exponenciálnej funkcie, ktorá sa zvýši na moc ročnej miery rastu do počtu rokov.
Matematicky je znázornený ako nižšie,
Konečná hodnota = Počiatočná hodnota * e Ročná miera rastu * Počet rokov.Výpočet exponenciálneho rastu (krok za krokom)
Exponenciálny rast možno vypočítať pomocou nasledujúcich krokov:
- Krok 1: Najskôr určte počiatočnú hodnotu, pre ktorú sa musí vypočítať konečná hodnota. Môže to byť napríklad súčasná hodnota peňazí vo výpočte časovej hodnoty peňazí.
- Krok 2: Ďalej sa pokúste určiť ročnú mieru rastu a je možné ju rozhodnúť na základe typu aplikácie. Napríklad, ak sa na výpočet budúcej hodnoty vkladu použije vzorec, potom miera rastu bude miera návratnosti očakávaná od situácie na trhu.
- Krok 3: Teraz je potrebné zistiť držbu rastu z hľadiska počtu rokov, tj. Ako dlho bude hodnota pod takou strmou trajektóriou rastu.
- Krok 4: Teraz určite počet zlučovacích období za rok. Zloženie môže byť štvrťročné, polročné, ročné, nepretržité atď.
- Krok 5: Nakoniec sa exponenciálny rast použije na výpočet konečnej hodnoty zložením počiatočnej hodnoty (krok 1) pomocou ročnej miery rastu (krok 2), počtu rokov (krok 3) a zloženia počtu za rok ( krok 4), ako je uvedené vyššie.
Na druhej strane sa vzorec pre kontinuálne zloženie používa na výpočet konečnej hodnoty vynásobením počiatočnej hodnoty (krok 1) a exponenciálnej funkcie, ktorá sa zvýši na hodnotu ročnej miery rastu (krok 2) do niekoľkých rokov (krok 3) ako je uvedené vyššie.
Príklad
Zoberme si príklad Davida, ktorý dnes na svoj bankový účet vložil sumu 50 000 dolárov za tri roky s 10% úrokovou sadzbou. Hodnotu vložených peňazí určte po troch rokoch, ak je zloženie zložené:
- Mesačne
- Štvrťročné
- Pol roka
- Ročne
- Nepretržite

Mesačné zloženie
Počet zložení za rok = 12 (od mesačného)
Výpočet exponenciálneho rastu, tj hodnoty vložených peňazí po troch rokoch, sa vykonáva pomocou vyššie uvedeného vzorca ako,

- Konečná hodnota = 50 000 dolárov * (1 + 10% / 12) 3 * 12
Výpočet bude

- Konečná hodnota = 67 409,09 USD
Štvrťročné zloženie
Počet zložení za rok = 4 (od štvrťroka)
Výpočet exponenciálneho rastu, tj hodnoty vložených peňazí po troch rokoch, sa vykonáva pomocou vyššie uvedeného vzorca ako,

Konečná hodnota = 50 000 dolárov * (1 + 10% / 4) 3 * 4
Výpočet bude

- Konečná hodnota = 67 244,44 USD
Polročné skladanie
Počet zložení za rok = 2 (od polroka)
Hodnota vložených peňazí po troch rokoch sa vykonáva pomocou vyššie uvedeného vzorca ako,

Konečná hodnota = 50 000 dolárov * (1 + 10% / 2) 3 * 2
Výpočet exponenciálneho rastu bude

- Konečná hodnota = 67 004,78 dolárov
Ročné zloženie
Počet zložení za rok = 1 (od ročného)
Výpočet exponenciálneho rastu, tj hodnoty vložených peňazí po troch rokoch, sa vykonáva pomocou vyššie uvedeného vzorca ako,

Konečná hodnota = 50 000 dolárov * (1 + 10% / 1) 3 * 1
Výpočet exponenciálneho rastu bude

- Konečná hodnota = 66 550,00 dolárov
Priebežné zloženie
Od nepretržitého zloženia sa hodnota vložených peňazí po troch rokoch počíta pomocou vyššie uvedeného vzorca ako,

Konečná hodnota = Počiatočná hodnota * e Ročná miera rastu * Počet rokov
Konečná hodnota = 50 000 dolárov * e 10% * 3
Výpočet exponenciálneho rastu bude

- Konečná hodnota = 67 492,94 dolárov
Kalkulačka
Môžete použiť nasledujúcu kalkulačku exponenciálneho rastu.
| Pôvodná hodnota | |
| Ročná miera rastu | |
| Počet zmesí | |
| Počet rokov | |
| Vzorec exponenciálneho rastu | |
| Vzorec exponenciálneho rastu | Počiatočná hodnota * (1 + ročná miera rastu / počet zloženia) počet rokov * č. zloženia | |
| 0 * (1 +0/0) 0 * 0 = | 0 |
Relevantnosť a použitie
Je veľmi dôležité, aby finančný analytik pochopil koncept rovnice exponenciálneho rastu, pretože sa primárne používa pri výpočte zložených výnosov. Enormnosť konceptu vo finančníctve demonštruje sila zloženia, ktorá vytvorí veľkú sumu s výrazne nízkym počiatočným kapitálom. Z rovnakého dôvodu má veľký význam pre investorov, ktorí veria v dlhé obdobia držania.