Skladacia definícia
Kompozícia je metóda výpočtu úrokovej sadzby, ktorá predstavuje efektívny úrok z úroku, pričom úrok sa počíta z investície / počiatočnej istiny plus zarobeného úroku a ďalších reinvestícií, inými slovami, získaný úrok sa kumuluje k sume istiny v závislosti od doby vkladu alebo pôžičky. to môže byť mesačne, štvrťročne alebo ročne
Pokúsme sa pochopiť, čo sa skladá a ako to funguje, pomocou niekoľkých základných príkladov
Najlepšie 4 príklady sily zloženia
Príklad č
Shane a Mark sa rozhodli investovať 1 00 000 dolárov, ale Shane sa rozhodol investovať do jednoduchého úroku, zatiaľ čo Mark investuje do zloženého úroku desať rokov s 10% úrokom. Pozrime sa, čo sa stane po desiatich rokoch.
Riešenie:
Výpočet Shaneovej investície bude teda -

Celková suma zárobku = 200 000 dolárov
S jednoduchým úrokom získa Shane po 10 rokoch 2,00 000 dolárov.
Výpočet investície do známky bude -

Celková suma zárobku = 2,59 374 dolárov
S úrokom Compound porastú Markove investičné hodnoty na 2 59 374 dolárov.
Teraz sa Shane rozhodol investovať pomocou metód zloženia, ako je Mark, a obaja investovali 2,00 000 dolárov so sadzbou 15%.
Výpočet Shaneovej investície bude -

Celková suma zárobku = 8,09 111,55 USD
Shane zostáva investovaný 10 rokov a získava konečnú sumu 8,09 111,55 USD s mierou 15%.
Výpočet investície do známky bude -

Celková suma zárobku = 65,83 790,52 dolárov
Mark je však dlhodobý investor trpezlivosť a zostáva investovaný 25 rokov a jeho investičná hodnota rastie na 65,83 790,52 dolárov
Vyššie uvedený príklad ukazuje silu zloženia. Čím dlhší je investičný horizont, tým väčší je exponenciálny rast.
Príklad č. 2 (týždenne)
Simon šetrí 7500 dolárov a pre univerzitný fond svojho syna, ktorý sa na univerzitu chystá po 15 rokoch, sa rozhodol investovať do amerických dlhopisov na sporenie. Simonovým cieľom je ušetriť 20 000 dolárov a ročná percentuálna miera pre americké sporiteľné dlhopisy je 6%. Aká je budúca hodnota Simonových peňazí po 15 rokoch?
Riešenie:
Vzhľadom na to,
- Riaditeľ = 7500 dolárov
- Sadzba = 6% alebo 0,06
- Časové obdobie = 15 rokov.
- Koľkokrát sa to zloží za rok n = 52 týždňov
- Budúca hodnota =?
Výpočet budúcej hodnoty bude teda -

Vzorec pre týždenné zloženie je uvedený nižšie.
F = P (1 + r / n) n * t- F = 7500 dolárov (1 + 0,06 / 52) 52 * 15
- F = 7500 dolárov (1 + 0,001153846) 780
- F = 18 437,45 dolárov
Z vyššie uvedeného výpočtu je teda zrejmé, že Simonov cieľ ušetriť 20,00 dolárov sa pomocou vyššie uvedených metód nedosiahne, ale je tomu bližšie.
Metóda kontinuálneho miešania
Teraz skúsime vyššie uvedený príklad s kontinuálnym zloženým vzorcom.
Výpočet budúcej hodnoty bude teda -

- F = 7500 $ 0,06 * 15
- F = 7500 $ 0,9
- Budúca hodnota (F) = 18 447,02 USD
Teraz ani pri Continuous Compounding nebude dosiahnutý Simonov cieľ, ktorým je úspora 20 000 dolárov na univerzitnom fonde jeho syna.
Pozrime sa s zloženou mesačnou formulou na to, koľko peňazí musel Simon investovať, aby dosiahol svoj cieľ ušetriť 20 000 dolárov za 15 rokov pri APR 6%?
Výpočet budúcej hodnoty bude teda -
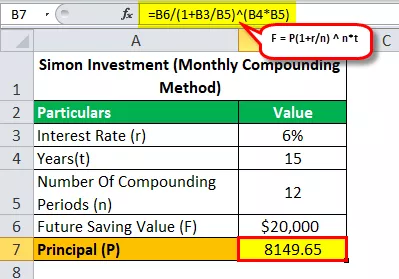
- 20 000 dolárov = P (1 + 0,06 / 12) 12 * 15
- P = 20 000 dolárov / (1 + 0,06 / 12) 12 * 15
- Istina (P) = 8149,65
Vyriešením vyššie uvedenej rovnice teda dostaneme odpoveď, ktorá je 8 149,65 dolárov (suma, ktorú musí Simon investovať, aby dosiahol svoj cieľ ušetriť 20 000 dolárov za 15 rokov).
Príklad č. 3 (efektívny anualizovaný výnos)
Povedzme, že banka s ručením obmedzeným XYZ dáva 10% ročne starším občanom na fixný vklad a tu predpokladáme, že úroky z banky sú štvrťročne zložené ako všetky ostatné banky. Vypočítajte efektívny anualizovaný výnos za 5, 7 a 10 rokov.
Riešenie:
Anualizovaný výnos na 5 rokov:
- t = 5 rokov
- n = 4 (štvrťročné zloženie)
- I = 10% ročne
Takže A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 za 5 rokov
Efektívny úrok = 0,6386/5
Účinné I = 12,772% ročne
Anualizovaný výnos na 7 rokov:
- t = 7 rokov
- n = 4 (štvrťročné zloženie)
- I = 10% ročne
Takže A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1,9965 za 7 rokov
- Účinné I = 0,9965/7
Účinné I = 14,236% ročne
Anualizovaný výnos na 10 rokov:
- t = 10 rokov
- n = 4 (štvrťročné zloženie)
- I = 10% ročne
Takže A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1,685 za 10 rokov
- Účinné I = 1,685 / 10
Účinné I = 16,85% ročne
Príklad č. 4 - (Anuity: budúca hodnota)
1 000 dolárov sa investuje každé 3 mesiace so 4,8% ročne, štvrťročne. Koľko bude mať Anuita hodnotu za 10 rokov?
Riešenie:
Takže keď hovoríme, koľko bude mať Anuita hodnotu za 10 rokov, znamená to, že tu musíme nájsť budúcu hodnotu, a to je dôležité, pretože kedykoľvek existuje príklad anuít, musíme zistiť, čo musíme zistiť.
Takže vzorec budúcej hodnoty je
FV anuity = P ((1+ r) n - 1 / r)- P = Periodická platba
- r = sadzba za obdobie
- n = počet období
Takže vzorec budúcej hodnoty je
- Takže tu P = 1 000 dolárov
- r = 4,8% ročne, alebo 0,048
- r (štvrťročne) = 0,048 / 4
- r (štvrťročne) = 0,012
- n = 10 rokov
- n (koľkokrát sa použije zloženie) = 10 × 4 = 40
Takže výpočet FV anuity bude -

Takže teraz FV = 1 000 $ (1 + 0,012) 40 -1 / 0,012)
Riešením vyššie uvedenej rovnice teda získate FV 50 955,30 USD
Koľko teda bude anuita za 10 rokov a odpoveď je 50 955,30 dolárov
Ako dodatočne môžeme z uvedeného príkladu zistiť, koľko úrokov sa získa za 10 rokov.
Pretože sa investuje 40-krát 1000 dolárov, ide o celkovú investíciu (40 × 1000 dolárov = 40 000 dolárov).
Takže úrok = budúca hodnota - celková investícia
- Úrok = 50 955,30 dolárov - 40 000 dolárov
- Úrok = 10 955,30 USD
Takže tu je dôležité pochopiť, že v Anuitách môžu investori získať veľký záujem. V uvedených konkrétnych príkladoch predstavuje vklad 40 000 dolárov na oplátku celkový úrok 10 955,30 dolárov.
Poznámka: Môžete si stiahnuť vyššie uvedenú šablónu programu Excel pre podrobný výpočet.








